Binomial in the Soccer field

“To be or not to be ..nomial”
- Statistical bad joke based on William Shakespeare, by me.

Source: Goalkeeper Sweety GIF, via GIPHY

Comment: Take a look here to the Jupyter notebook with the calculations and simulations of this blog.

In Mexico there are two specific things you probably have learn since kid: eat Chile and play Soccer. The first one is optative, the second is required. Therefore, you could unknow a lot of important things in life -as math, biology or statistics- but for sure you would know about soccer.

Personally, I am not a huge soccer fan like my father, father in law, friends, co-workers or even wife, but each 4 years I dust off my green-jersey from 1998’s Mexico soccer team and almost religiously follow the World Cup games.

In the soccer field, over last World Cups, the national team has been playing quite-good until they meet the Penalty Shootout, where it looks like the team has been cursed for many many years.

Recently, I read an interesting article$^1$ related with our National Team’s headache, Penalty Kicks… by the Numbers from Jay Williams, who talks about different statistic related with different soccer leagues and championships. In Williams’ article, one specific number jumped to my sight when I read the next sentence:

“From the penalty kicker’s standpoint, 85% of the penalty shots placed on goal were successful”.

As a Mexican who feel that his National Team is cursed, and as a future Data Scientist, I feel the duty of study -and share with you- the probability of winning a game by scoring as much goals as possible in the Penalty Shootout.

However, in the case of Mexico, I felt that this effective soccer goals rate probably was lower, so I look for some statistics from transfermarkt.com and calculate that about 73% of the penalty shots placed by the Mexican team were successful.

And here is where the Binomial distribution enter the soccer field. The binomial distribution helps us to obtain the probability distribution of k number of successes from a total of n independent trials, where each one event has a p probability of success. The formal formula (1) is expressed after this paragraph. If you are interested to know more about this statistical Binomial distribution I recommend you to visit Binomial Distribution in Wikipedia

From this point, if I suppose 4 of 5 successful penalty shootout are a good score, I would be interested in obtain the probability that the Mexican team scores 4 goals in a penalty shootout of 5 penalty kicks, assuming a 0.73 probability of score a goal. If I plug in these numbers, the formula looks like $\binom{5}{4} {0.73}^4 (0.27)^1$ …returning a 38% probability that my green team would score 4 out of 5 penalty kicks in a shootout!

If we go further and obtain the complete Binomial distribution, we could find that the probability of scoring 4 or more goals in a penalty shootout for the Mexican team is 59%.

This doesn’t sound as bad. However, if replicate the previous process assuming the p of 85% of success for score a penalty kickout mentioned by Jay Williams, we would find out that the probability of scoring 4 or more goals in a penalty shootout for an average team is equal to 84%.

So when we compare these successes rates in scoring 4 out of 5 penalty kicks in a penalty shootout from Mexico (59%) vs. the average team (84%), we only thing that comes to my mind is that my greens should keep training penalty kicks!

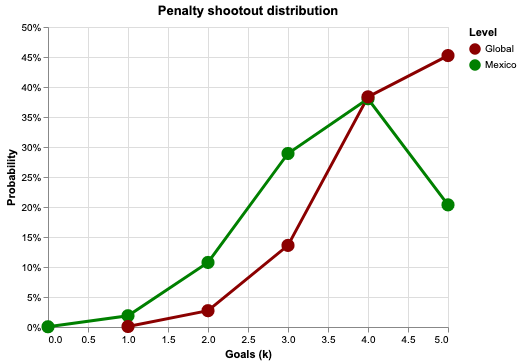
Source: Jupyter Notebook of the Binomial in Soccer field, 2020, by Vic Cuspinera.